両辺の次元は必ず一致していなければならない。 例えば、ニュートンの運動方程式はF = ma と書かれる。この式は、次元・単位について、左辺の「力」 が質量と加速度の積となることを主張している。力の単位はN(ニュートン)であるから、これは次の関Amazonでの次元のすべて 改訂第2版 (ニュートン別冊)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。また次元のすべて 改訂第2版 (ニュートン別冊)もアマゾン配送商品なら通常配送無料。2 ニュートンの運動方程式 6 2 ニュートンの運動方程式 21 座標 質点P は直線上を動いているとする。 この点P の座標をx とする。 そして、このx は時刻t によって定 まると考え、次のように表す。 x = f(t) さて、文字を節約して次のように表わすことにする。
4次元
ニュートン 次元
ニュートン 次元-AmazonでのNewtonライト 次元 (ニュートンムック)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。またNewtonライト 次元 (ニュートンムック)もアマゾン配送商品なら通常配送無料。ニュートン別冊 次元のすべて 私たちの世界は何次元なのか? 品切 Amazonでのご購入はこちら ISBN 変型判並製/カラー4色刷/176ページ 発行年月日:19年1月5日 定価:本体1,800円+税 ツイート 読者アンケートに答える 世紀のはじめ,アインシュタインはこの宇宙が「3次元の空間」と「1次元の時間」からなる「4次元時空」であることを示しました。 ところ



次元のすべて 改訂第2版 ニュートン別冊 Heiman 通販 Yahoo ショッピング
マクロな力学的な量である角運動量の場合, 単位は N・m・s(ニュートンメートル秒)とした方がしっくり来る それには理由がある 先ほど力のモーメントとエネルギーは同じ次元だという話をしただろう しかし物理的意味合いは異なるため, 力のモーメントの単位は J(ジュール)ではなく, あくまでも N・m (ニュートンメートル)としておくべきなのだ 同様に, 角運動量は運動Amazonでのご購入はこちら ISBN A5判/カラー2色刷/128ページ 発行日:年10月15日 定価:本体900円+税 読者アンケートに答える 「次元」とは,何でしょうか。 ごく簡単にいえば,次元とは動くことができる方向の数のことです。 私たちの世界では,縦,横,このとき、ニュートン法の計算式は x k1 = x k u (x k) = x k J (x k)1 f (x k) となる。ここに、 J (x k) はヤコビ行列と呼ばれ、 であり、また、 u (x) = J (x)1 f (x) である。 2変数の場合は、逆行列が簡単に求められるので ここに
432 ロジスティック回帰の実装:入力が2次元の場合 ニュートンラフソン法によるロジスティック回帰の最尤推定を実装します。 利用するライブラリを読み込みます。 # 4323項で利用するライブラリ import numpy as np from scipystats import multivariate_normal # 多 1次元ニュートン法のプログラム 以下のプログラムは、1次元のニュートン法のプログラムで、 方程式 x^24 = 0 を初期値 x_0=3 から始めて解くプログラムです。 このコードを動かすと、ステップを繰り返すごとに急激に解に近づいていっていることが分かります。 (デフォルトではコメントアウトしてあります。 ) $ gfortran mainf90 $ /aout 1 2 ニュートン newton N m⋅kg⋅s2 この表の中で,平面角をあらわすラジアンと立体角をあらわすステラジアンが無次元となっている. ラジアンは円の半径と円弧の長さの比により定義されるので,m/m より無次元となる.
ニュートン法の近似開始値 に対して この をそのまま解の1つ目の実数解として利用する 近似開始値が、極値をとるxであった場合 この場合、ニュートン法が収束しなくなるので、別の近似開始値 を使うよううながす。私のプログラムでは01加えるようにニュートン別冊 次元のすべて 改訂第2版 ホログラフィー理論がみせる次元の新しい世界 Amazonでのご購入はこちら ISBN 変型判並製/カラー4色刷/176ページ 発行年月日:年12月5日 定価:本体1,800円+税 読者アンケートに答える この世界が何次元空間かと問われたら,縦・横・高さからなる「3次元空間」と答えるのが普通だと思います。 ところが物理学の最 ニュートン法による計算は収束が速く(つまり少ない回数で解にたどりつくことができ)、\( 2\)回の計算で数値解\( x=\)を得た。 scipyoptimize による計算とは若干異なっているが、これはどのくらいの精度になったら計算を停止するかという設定が



求根アルゴによる非線形方程式の解 Thoth Children




Newton別冊 次元のすべて ニュートンムック Hmv Books Online
124 n 次元n 変数方程式に対するNewton 法 141 表121 Newton 法の収束(1 次元, IEEE754 倍精度計算) k xk 0 1 2 3 4 となる。 08年4月に刊行したNewton別冊「次元とは何か」は,たいへん好評をいただきました。 このたび,不思議な次元の世界をさらにわかりやすく紹介するため,完成度を高めた"増ページ改訂版"を刊行することとなりました。 私たちは,縦・横・高さでつくられた3次元空間に加え,1次元の時間を合わせた,「4次元時空」に住んでいると考えています。 しかし,今,科学者たちの間 で 赤の曲線が元の関数 f で,青の 2 次関数が近似した曲線になります.それでは,ニュートン法を Python で実装して停留点を与える解を求めます.本記事では, scipyoptimize など便利な API は敢えて使わずに作ります. newton_1vpy




ニュートンの運動の第二法則 Labster Theory
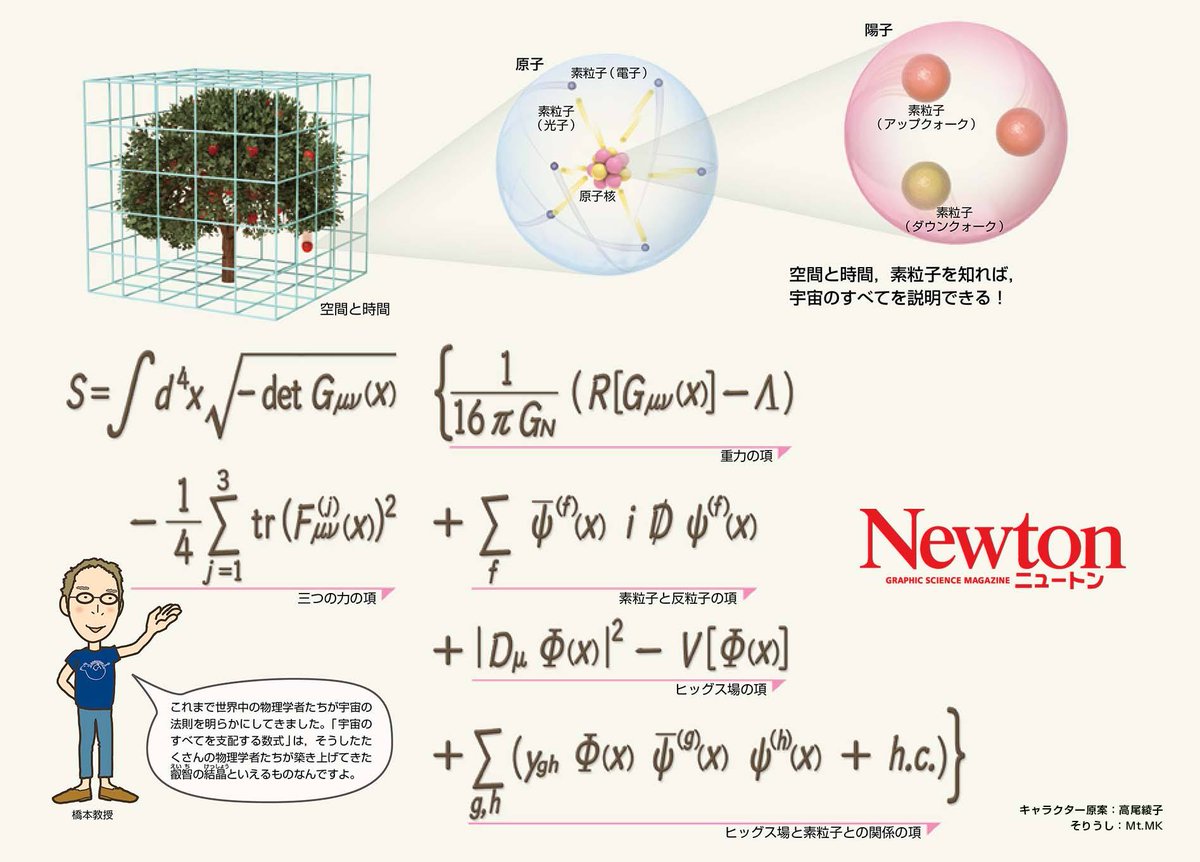



科学雑誌newton ニュートン 公式 これが 宇宙のすべてを支配する数式 です D X インテグラル ディー 4乗 エックス は その後ろにつづく関数を 宇宙全体 つまり3次元空間と時間のすべてで 足し合わせる 積分する ことを意味します 発売
まとめ:1ニュートンは1kgの物体を1秒間に毎秒1mの速さずつ速くする力のこと 以上が力の単位ニュートンだね。 色々グダグダ言ってきたけど、中学理科では、 100gの物体に働く重力の大きさが1ニュートン と覚えておけば大抵の問題を計算できるはずだ定義 国際単位系 (SI) 及び日本の計量法におけるジュール J の定義は以下の通り。 1 ニュートンの力がその力の方向に物体を 1メートル動かすときの仕事; ニュートン法の考え方 ニュートン法では、以下の考え方に基づいて計算が行われます f (x) = 0になるような値xを探す時、ある値x1における接線の切片x2は、元の値x1より真の値xに近くなる この考え方は下の図のように、f (x)という関数においてf (x) = 0になる




ヤフオク 送料無料 3冊 ニュートン別冊 4次元宇宙の謎



次元のすべて 私たちの世界は何次元なのか ニュートンプレス 版元ドットコム
Newtonライト 次元 想像をこえる高次元の世界へ 次元 21年2月刊行の「Newtonライト」は,『次元』です。 私たちは,縦・横・高さからなる「3次元」の空間に住んでいます。 そう聞いて,異論をとなえる人はいないと思います。 では,そもそも「次元」とは何なのでしょうか。 この本では,1次元から順番に,2次元,3次元と考えていきます。 そうすると,4次元の世界も想像し 一方、 ニュートンとは力の大きさを表す単位のこと です。 例えば、ボーリングの球を持っているとします。 そうすると、重いと感じますよね? 重いと感じるのはボーリングの球が地球からの重力により引っ張られているからです。 その重いと感じる度合い(力の度合い)をニュートン(N)を使って表します。 ちなみに 重さとは、重力の大きさのことで す。 当然、 ニュートンは 一方、次元とは4つの基本となる単位(長さ、質量、時間、電流)をどれだけ掛けたかを表しており、Nの場合は質量×長さ×時間^(2) の次元を持っています。 そして本質的に同じ種類の物理量は必ず同じ次元を持っています。 物理学の単位はすべて次元を持っており、単位が分かればその物理量の次元が分かります。 けれども単位は次元そのものではありません。 力の単位である




ヤフオク 送料無料 3冊 ニュートン別冊 4次元宇宙の謎




ニュートン式 超図解 最強に面白い 次元 ニュートンプレス Hmv Books Online
Pa(パスカル)とN(ニュートン)は直接は換算できない1Nは何Pa?1Paは何N 結論からいいますと、 Pa(パスカル)とN(ニュートン)は直接的には変換できません 。 これはPaの定義を考えていく理解しやすいです。これはニュートン形式の運動量に一致する。 極座標系 一般化座標として二次元極座標 x = (r, θ) を選ぶと、ラグランジアン及び r, θ に共役な運動量 p r, p θ はそれぞれ次元 ユークリッド空間 での場合はファイン(Fine)によって1916年に示された。 その後、 バナッハ空間 での半局所収束定理が カントロビッチ (Kantorovich)によって1948年に示され、現代では ニュートンカントロビッチの定理 と呼ばれている 。 この定理にはいくつかの変種が知られており、 にまとめられている。 高次元の場合 ニュートン法は、接線を一次近似式、接線の x 切片を一次近似




Pythonによる科学 技術計算 4次のルンゲ クッタ法による1次元ニュートン方程式の解法 Qiita




ニュートン単位って何なの ニュートン キログラムに換算してみよう 自分で作ろうインダストリアルな空間を
解答 上のニュートン粘性の法則の定義式に従います。 τ = 1000 × (001 / 01) = 100Paとせん断力が求められました。 きちんとニュートン流体に性質について理解しておきましょう。 関連記事 粘度と動粘度とは? ニュートン粘性の法則の導出と計算方法 Pythonで数値計算プログラムを書き直そうシリーズ 「ここ、こうすればいいのに」とかあれば教えてください(土下座) はじめに 非線形方程式の数値解法と言えば、Newton法が二分法と並んでよく取り上げられます。関数の傾きを多次元ニュートン法 野下浩司 多次元ニュートン法を用いて,被食捕食系の平衡点を見つけることを目指す.ここで は出来るだけ簡単な方法でプログラムを書こう. 1 解きたい問題 被食捕食系 8 >>> >>< >>> >> dx dt = ax bxy (1) dy dt = cxy dy (2)




Newton ニュートン 18年 4月号 Newton編集部 Hmv Books Online




ヨドバシ Com 次元とは何か 改訂版 0次元の世界から高次元宇宙まで ニュートンムック Newton別冊サイエンステキストシリーズ ムックその他 通販 全品無料配達
ニュートン流体の応力による変形 2 次元の粘性流体(ニュートン流体)において,せん断応力や圧力はどのような形で表されるかをみていきま す。流れの中にx,y 座標をとり,それぞれの速度成分をu,v とすると,流体の変形はdu,dv によって生じるこ ニュートン法、ホーナー法で、解の近似値を発散させない方法は? : ニュートン法・ホーナー法では、近似の初手として選び出す推定値である a1 の採り方がまずいと、解 α = a∞ の数値が発散して、近似に失敗するそうですが、それを避ける為の必勝Amazonでのニュートン式 超図解 最強に面白い!!次元 (ニュートン式超図解 最強に面白い!!)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。またニュートン式 超図解 最強に面白い!!次元 (ニュートン式超図解 最強に面白い!!)もアマゾン配送商品なら通常




ニュートン法 1 2次元 多次元 シキノート



ニュートン法による求根 Thoth Children
Amazonでの次元とは何か―0次元の世界から高次元宇宙まで (ニュートンムック Newton別冊サイエンステキストシリーズ)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。また次元とは何か―0次元の世界から高次元宇宙まで (ニュートンムック Newton別冊ここで, 左辺の F と右辺の垂直抗力 N はどちらもニュートンという単位 ( N = kg ⋅ m / s 2 , 次元は MLT − 2 )を持っているので, μ ′ は 次元を持っていてはいけない つまり, μ ′ = F N という 同じ次元を持つ物理量同士の比率を表す量は無次元量である 別の例としては, 角度 θ を表す単位である ラジアン ( rad ) も無次元量である ラジアンの定義は扇型の弧の長さ l を扇型の半径 r で割った量である ( 弧ジュールはSI組立単位であり、 N m 又はSI基本単位を用いて kg m 2 s2 と表記される 。 ジュールと形式的には同じ単位を力の



Se Fukuoka U Ac Jp




4次元空間を 見る 方法とは 科学雑誌newton ニュートン Facebook
と,図4のようなニュートン法のフローチャートが考えられる.なお,漸化式を取扱う場 合,一次元配列を利用すると便利である. ü i û ó Á o Æ é&v 2 o $ ü äÒå¿ã$ &³ 4 ニュートン法のフ次元のすべて 改訂第2版 (ニュートン別冊) ¥1,980 在庫あり。 購入を強化する 世紀のはじめ,アインシュタインはこの宇宙が「3次元の空間」と「1次元の時間」からなる「4次元時空」であることを示
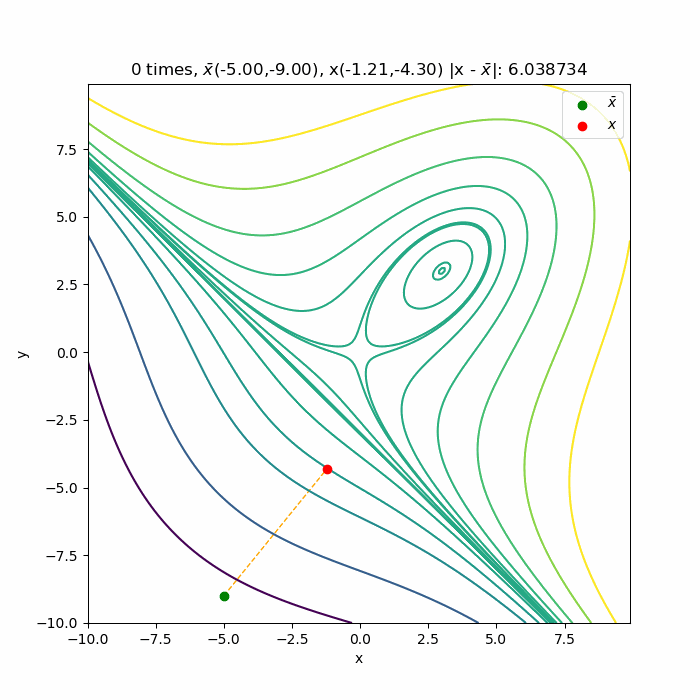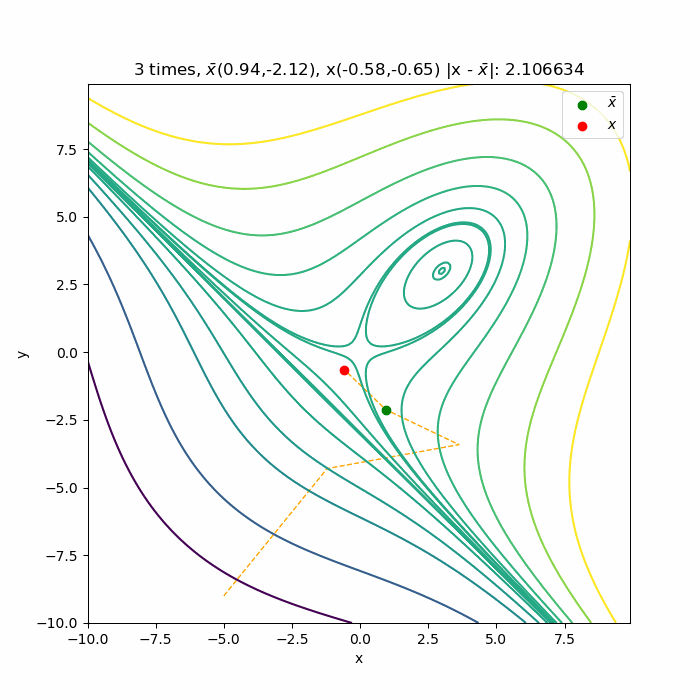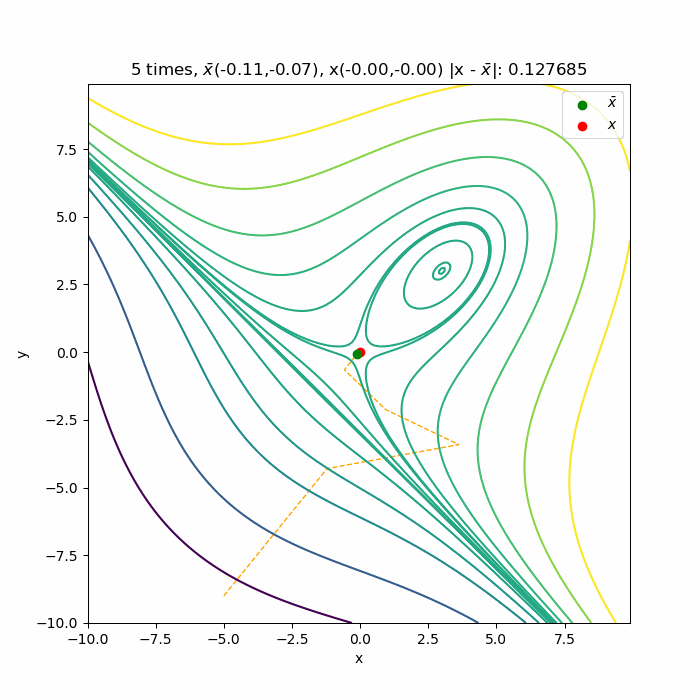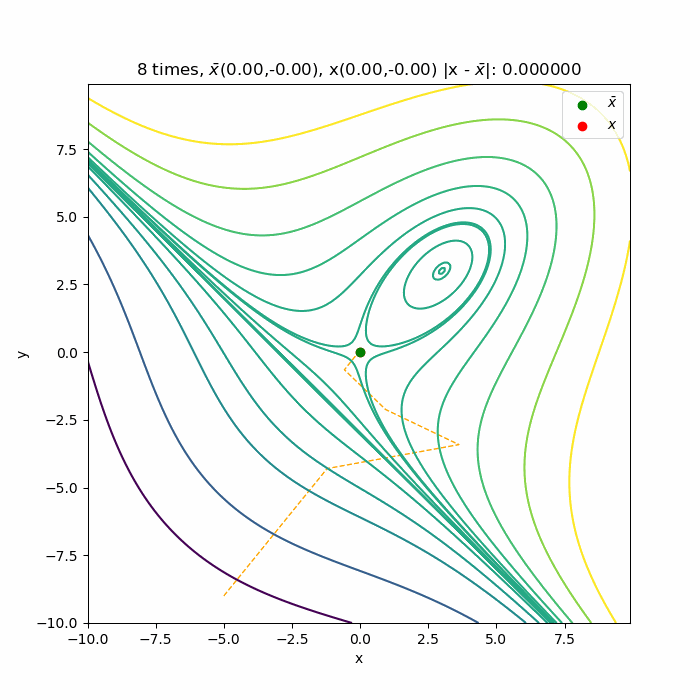



多変数のニュートン法の収束の様子を可視化 仕事と投資とあと何か
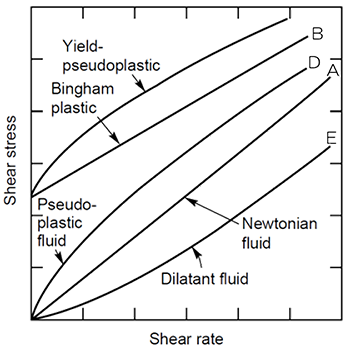



熱流体コラム 非ニュートン流体の1次元解析 Engineering Eye 伊藤忠テクノソリューションズの科学 工学系情報サイト




優先配送 ニュートン 月刊誌 Newton 趣味 スポーツ Chescotimes Com



Newton 別冊 宇宙の終わり ニュートンプレス 版元ドットコム




別冊 高次元の物理学 ニュートンプレス



2次元チャンネル流れ 非ニュートン流体




ニュートン法 Wikipedia
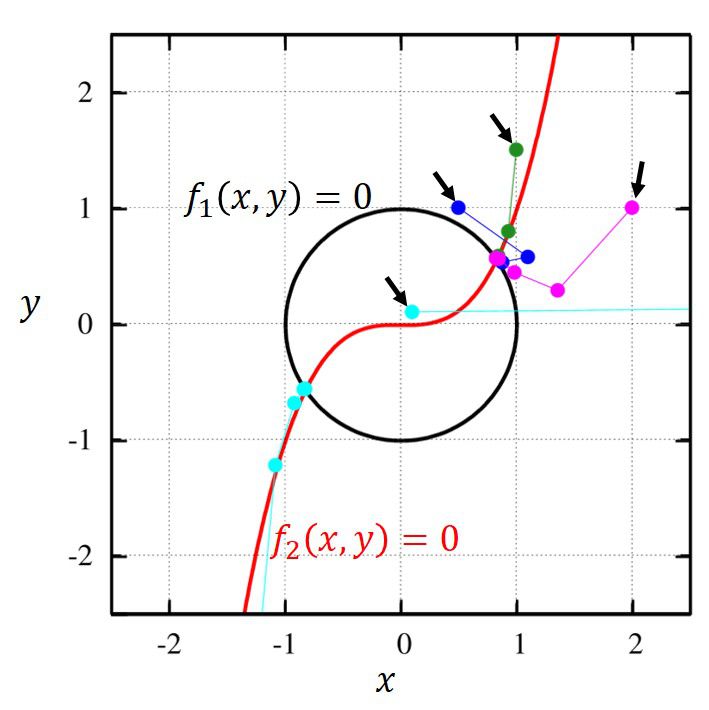



ニュートン法 1 2次元 多次元 シキノート




次元とは何か 改訂版 ニュートンプレス




相対性理論9冊セット Newton 四次元 時空 超ひも理論 宇宙のはじまり 時間論 ブラックホール アインシュタイン 量子力学 ニュートン の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




高次元 Japanese Edition Ebook 科学雑誌newton Amazon Fr Boutique Kindle




村田次郎 Jiro Murata 別冊newton 次元 のすべて 改訂第2版が届きました 相対性理論から超ひも理論まで 三次元を超える高次元の物理をsfではなく 大真面目に正面から紹介したビジュアルたっぷりの刺激的な一冊になっていると思います 僕の実験も丁寧




2次元ニュートン法による円と円の交点の数値計算 Qiita



4次元




理学部の村田次郎教授が科学雑誌 Newton の巻頭特集に登場 立教大学




英国王立協会 ニュートンが4次元時空の着想を得ていたことを発表 とね日記




Newton ニュートン 17年11月号 高次元空間を見つけ出せ 想像を絶する惑星たち 再生医学の最前線 3 臓器を細胞から組み立てよ の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




11次元 超弦理論による次元の数 数字で見る It Insight Best Engine




4次元宇宙の謎 改訂版 時間と空間の最新像にせまる ニュートンムック newton別冊 ニュートンプレス その他 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
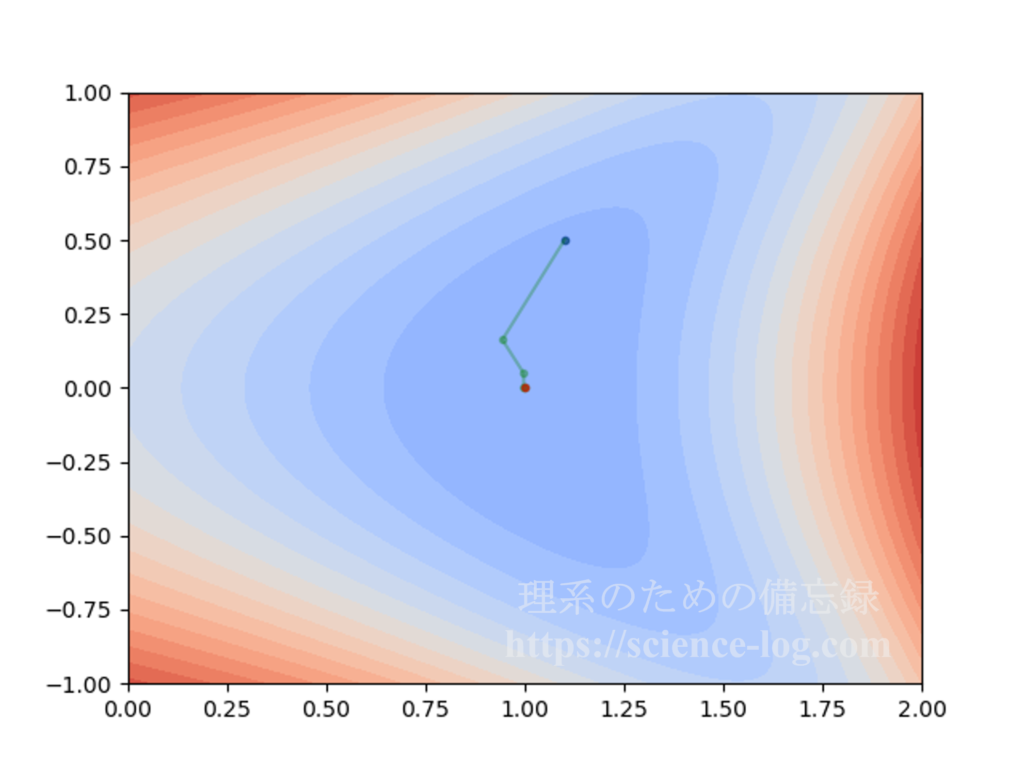



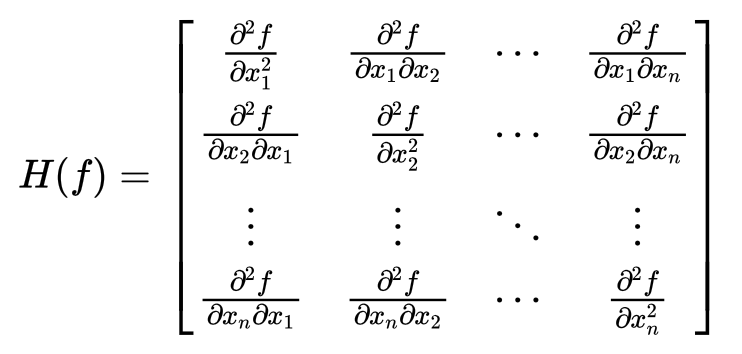
最適化問題の基礎 ニュートン法とヘッセ行列 理系のための備忘録




全ての Newton 別冊 次元のすべて 改訂第2 版 在庫有




Newton 別冊 次元の中古 未使用品 メルカリ




リブリオエッセイ ことばの次元 ぼくの因縁 韻踏んでますねん しおん横須賀すとうりぃ 宇宙と花とつながる言葉




Newton ニュートン 17年1月号 発売日16年11月26日 雑誌 定期購読の予約はfujisan
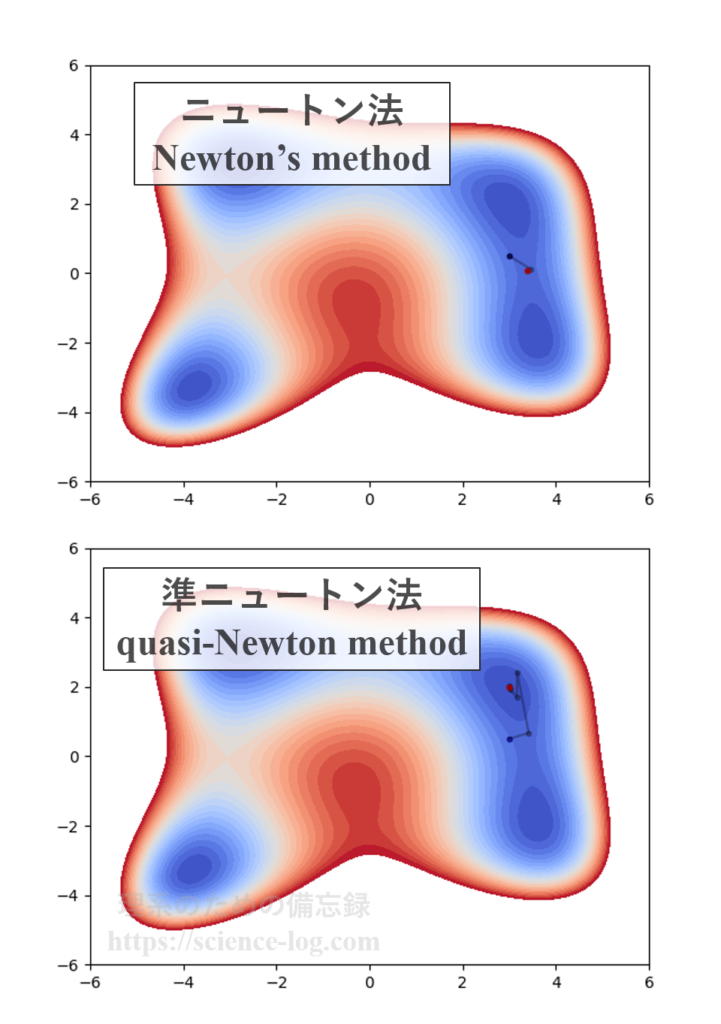



最適化問題の基礎 準ニュートン法とセカント条件 理系のための備忘録




ニュートン 次元とは何か メルカリ




ニュートン式 超図解 最強に面白い 次元 ニュートンプレス




綾瀬市にてnewtonなどを買取りしました 神奈川書房




優先配送 ニュートン 月刊誌 Newton 趣味 スポーツ Chescotimes Com




科学雑誌ニュートン 17年11月号 ニュートンプレス




橋本幸士 Koji Hashimoto Pa Twitter ニュートン別冊 高次元の物理学 がついに解禁 T Co Ehiogy5ych Newton Science 取材協力させていただきました 包括的に高次元の物理学が身近に感じられる別冊特集 素晴らしい T Co Y9k14b1hwh




科学雑誌newton ニュートン Facebook
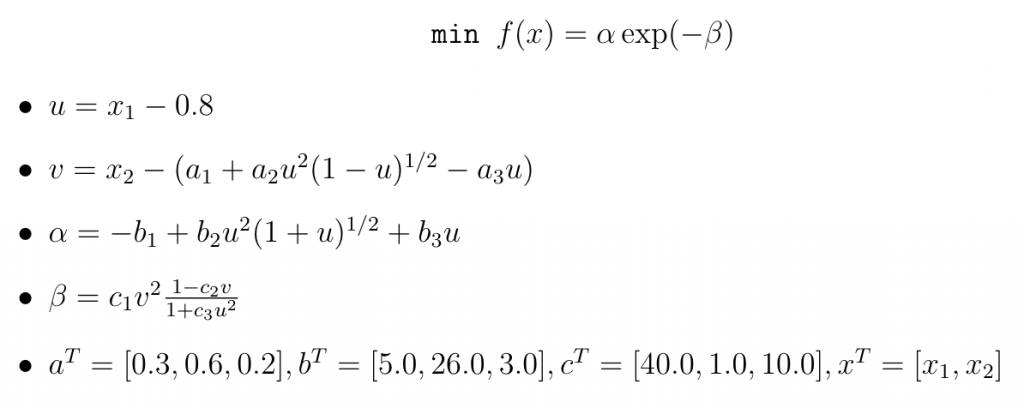



Pythonでやる多次元ニュートン法 Miidas Research




科学雑誌newton ニュートン 4次元をイメージしてみよう 発売中のnewton最新号 16年1月号 では 高次元 の世界 と題して 3次元をこえる高次元空間 を特集しています 特集のテーマになっている 高次元空間 について 考えたことはありますか
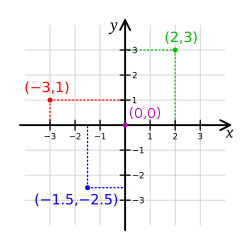



ニュートンの 時間 と 空間 と 座標 の定義 2 デカルト座標 1次元 2次元 3次元 量子力学と意識の変容 宇宙と人間の無限性について




Newton別冊 超ひも理論と宇宙のすべてを支配する数式 By 科学雑誌newton
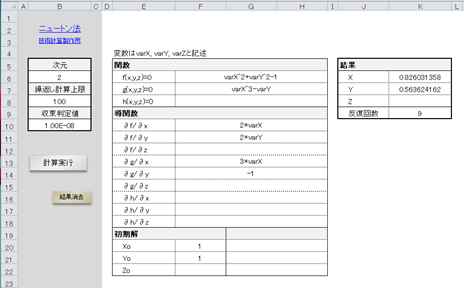



技術計算製作所 ニュートン法 Excel Vba 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Excel Numcal Newton




相対性理論9冊セット Newton 四次元 時空 超ひも理論 宇宙のはじまり 時間論 ブラックホール アインシュタイン 量子力学 ニュートン の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




喜久屋書店仙台店 キクちゃん ニュートン プレス Newtonライト2 0 元素とイオン Newtonライト2 0 次元 入荷しました T Co Gawgert4yv Twitter
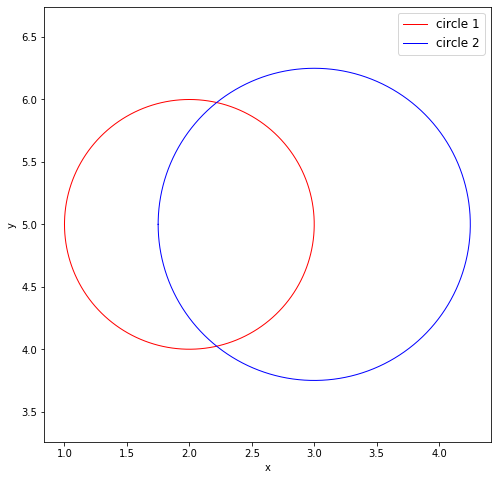



2次元ニュートン法による円と円の交点の数値計算 Qiita




ニュートン 次元とは何か メルカリ



Newtonライト3 0 超ひも理論 ニュートンプレス 版元ドットコム




ニュートン 次元の中古 未使用品 メルカリ



2



コラム 運動方程式は古典力学の全てだ とある博士が物理の入試問題を解いてみたらこうなった件




心理学専攻大学院生の和崎夏子さん 橋本悠那さんが作成した図版が Newton別冊 ゼロからわかる心理学 錯覚の心理編 に掲載されました 学科ブログ 日本女子大学 心理学科 オリジナルwebページ



Kakeru Movie



次元のすべて 改訂第2版 ニュートン別冊 Heiman 通販 Yahoo ショッピング




Newton ニュートン 17年11月号 高次元空間を見つけ出せ 想像を絶する惑星たち 再生医学の最前線 3 臓器を細胞から組み立てよ の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
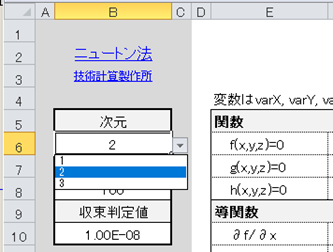



技術計算製作所 ニュートン法 Excel Vba 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Excel Numcal Newton




2次元ニュートン法による円と円の交点の数値計算 Qiita



エッセイ集 ずぼらぐうたら軽楽すとれっちーず 高次元と序列の話 Powered By Line



詳細表示



これが今年のトピックスだ 人工ブラックホール 高次元宇宙の存在証明 ニュートン編集部が大予想 03




Newtonライト2 0 超ひも理論 By 科学雑誌newton



時間はなぜ1次元 Newton ニュートン ミユウのいろいろ日記




ニュートン式超図解 Twitter Search Twitter




次元とは何か 0次元の世界 から 高次元宇宙 まで ニュートンムック Newton別冊サイエンステキストシリーズ Amazon Com Books




Newton別冊 次元のすべて ニュートン別冊 本 通販 Amazon
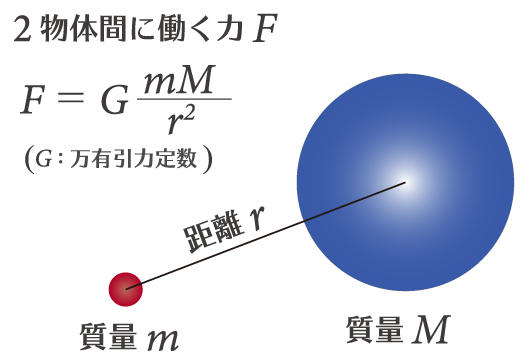



空間はほんとうに 縦 横 高さの三次元だけで できている Kek Imss




ニュートン 次元の中古 未使用品 メルカリ




楽天ブックス 次元のすべて 私たちの世界は何次元なのか 本




超ひも理論 橋本幸士監修 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




Newton 別冊 次元の中古 未使用品 メルカリ




Newton ニュートン 17年11月号 高次元を見つけたぜ ゼロからわかるうつ病 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




ニュートンaの評価 適正 Ss倍率をモンスト攻略班が徹底解説 ユーザーの評価 反応も Appbank
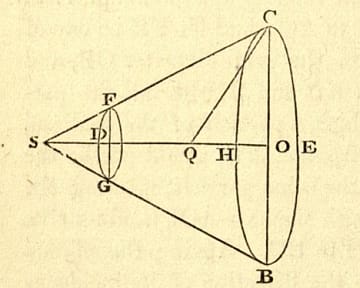



英国王立協会 ニュートンが4次元時空の着想を得ていたことを発表 とね日記




次元のすべて 改訂第2版 ニュートンプレス



Pythonでやる多次元ニュートン法 Miidas Research




ニュートンの運動方程式の極座標表示 2次元 倭算数理研究所




Newton 02




ヤフオク 4次元宇宙の謎 改訂版 ニュートンプレス




Jiro Murata



次元 って何 Newton ニュートン ミユウのいろいろ日記




最適化問題の基礎 ニュートン法とヘッセ行列 理系のための備忘録
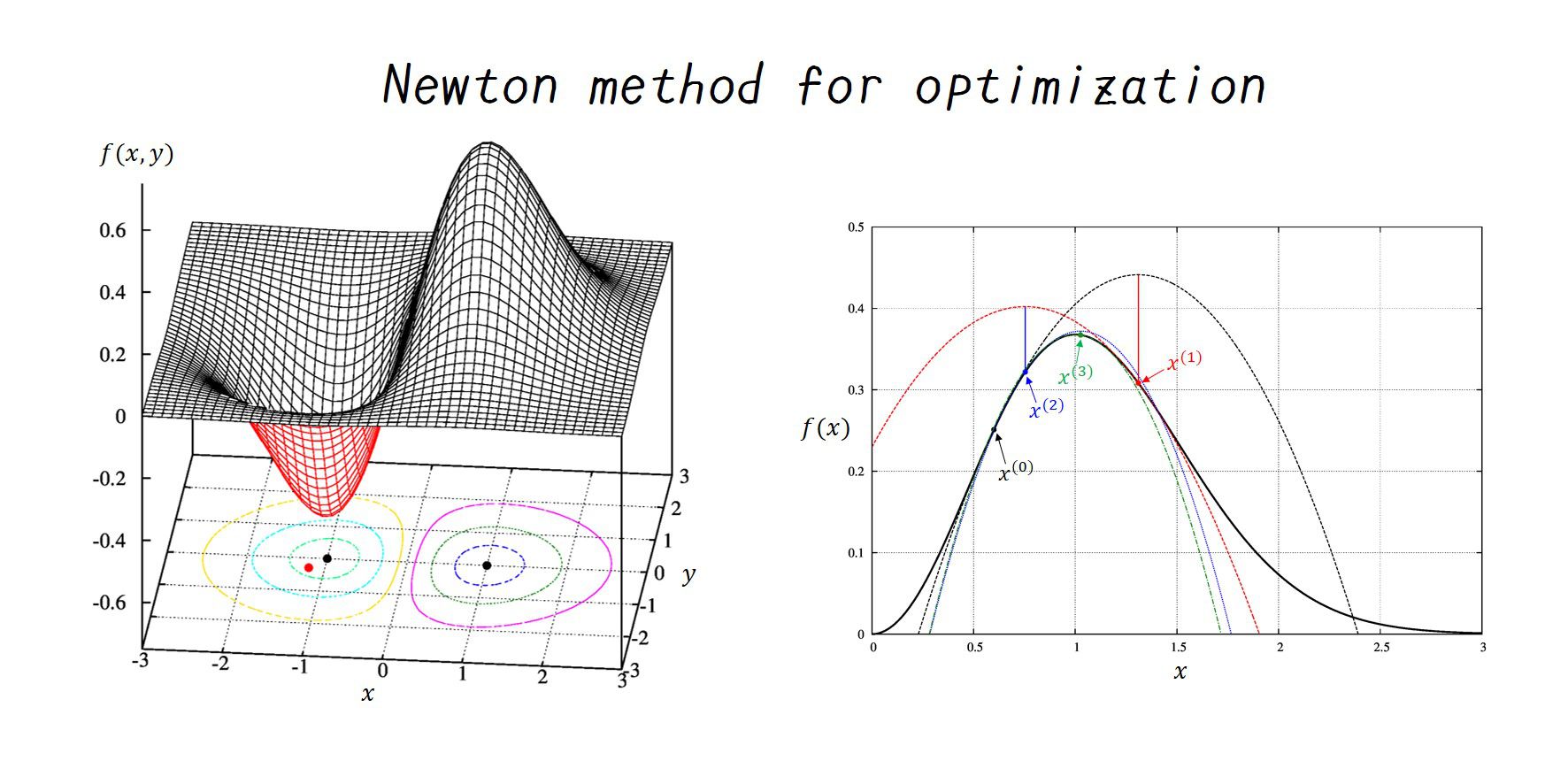



極値を求めるニュートン法 シキノート




楽天ブックス 次元とは何か 0次元の世界 から 高次元宇宙 まで 本




ニュートン 18 4月号 Lalala Web Co Jp




村田次郎 Jiro Murata 別冊newton 次元 のすべて 改訂第2版が届きました 相対性理論から超ひも理論まで 三次元を超える高次元の物理をsfではなく 大真面目に正面から紹介したビジュアルたっぷりの刺激的な一冊になっていると思います 僕の実験も丁寧




見えない次元は どこにかくれているの 科学雑誌newton ニュートン Facebook



Kakeru Movie



2




Newton ニュートン 別冊 次元とは何か 08年 メルカリ




書籍 次元 想像をこえる高次元の世界へ ニュートンムック 理系脳をきたえる Newtonライト2 0 ニュートンプレス キャラアニ Com




Newtonライト2 0 次元 ニュートンムック 本 通販 Amazon



0 件のコメント:
コメントを投稿